Tensegrities
Uit Arthesis jaargang 16 nummer 1 & 2
De hierbij afgebeelde toren, ongeveer 4,5 meter hoog, heb ik op bijeenkomsten van gebruikers van computer-programma’s, gebaseerd op de Eindige-Elementen-Methode, gebruikt om resultaten van die programma’s te verifiëren. Een dergelijke toren staat ook in mijn voortuin (figuur 1).
Omdat constructies meer gaan leven als er achtergrondinformatie beschikbaar is en ik dan tevens voorkom telkens hetzelfde verhaaltje te moeten vertellen, wil ik in dit artikeltje het ‘hoe en waarom’ van deze toren beschrijven.
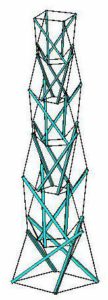
Waarom?
In een technisch tijdschrift van eind jaren ’60 stond een artikel over de wonderlijke toren van Kenneth Snelson. In de beeldentuin van het Kröller-Müller museum op De Hoge Veluwe was die zomer zijn zogenaamde ‘Needle Tower’ geplaatst. Deze wonderlijke toren rees, ongetuid doch stabiel, tot 18 meter recht omhoog. Hij bestond uit 10 x 3
drukstaven verbonden door een 90-tal spankabels. (Velen van u zullen hem in die beeldentuin wel eens hebben gezien; in Arthesis 15/2 op pag. 12 is Snelsons ‘Needle Tower II’ te zien, n.a.v. de tentoonstelling Schaal en Maat). Tot zover geen bijzonders, echter de laatste zin in dat artikel stond mij niet aan:
Kenneth Snelson beweert dat geen ingenieur in staat zou zijn dit te berekenen.
Wat berekenen betreft bedoelde hij de sterkte en de stijfheid. Zoiets moet je natuurlijk niet tegen een constructeur zeggen! We zullen wel even laten zien dat zo’n ruimtelijke constructie met de huidige computer-programmatuur eenvoudig te berekenen is.
Op dat moment had ik echter geen tijd om een proefje te doen. Jaren later, in de winter van 1978, herinnerde ik me dit probleem. Even het bewuste artikel zoeken; natuurlijk nergens te vinden! Dan maar zelf een torentje bedenken. Ik herinnerde me wel dat de toren uit alléén trek- en drukstaven bestond, en dat de drukstaven elkaar niet raakten. Overigens, trekstaven zijn draden, kettingen e.d., drukstaven zijn buizen, stokken e.d. Ga je gang …..
[read more=”Lees meer” less=”Lees minder”]
Hoe?
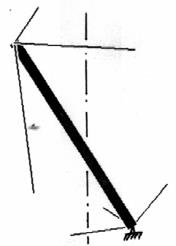
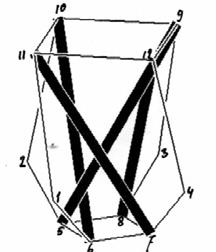
Een mast kun je tuien met drie draden; meer hoeft niet, minder kan niet. Als je de onderkant van deze mast of stok nu niet op de grond zet maar ook in drie draden ophangt, staat hij stabiel in de ruimte. Zie figuur 2. Door nu deze ene mast met zes draden 0, 90, 180 en 270 graden te draaien om de verticale stippellijn ontstaat figuur 3.
Figuur 3 is nu één etage van de toren. Natuurlijk zijn de lengtes van de draden t.o.v. de stokken niet willekeurig. Met een beetje mechanica-kennis zie je dat bijvoorbeeld punt 1 in een vlak door de punten 7-11-9 moet liggen. Met dit gegeven is het mogelijk alle knopen in ruimtelijke coördinaten vast te leggen. Met het vastzetten van de punten 1 t/m 4 staan de vier stokken stabiel in de ruimte en kan ik bijvoorbeeld de bovenkant van de stokken (punten 9 t/m 12) als steunpunt voor de volgende etage gebruiken.
Dit soort constructies heet tensegrities (tensional integrities). Anthony Pugh geeft in zijn boek An introduction to tensegrity de volgende definitie: ‘A tensegrity system is established when a set of discontinuous tensile compressive components interacts with a set of continuous tensile components to define a stable volume in space.’
Zelf heb ik daaraan toegevoegd: a minimum number of tensile components. Dat wil dus zeggen dat iedere stok met zes draden is verbonden en niet meer. Snelson gebruikt meestal acht en soms zelfs tien draden per stok. Dat is dus te veel. Je kunt dat aan zijn ‘Needle Tower’ dan ook zien, er hangen een aantal draden slap, die heb je dus niet nodig! Een nadeel van mijn minimum number of tensile components is dat als er één stok breekt of één draad doorroest de toren in elkaar stort! Dat is dan ook ooit gebeurd.
Berekening
De aanleiding voor dit geheel was de opmerking van Kenneth Snelson dat een constructeur dit soort torens niet kan berekenen. Het moge duidelijk zijn dat het mij uiteindelijk gelukt is de sterkte en stijfheid van dergelijke constructies te berekenen. Het bewijs daarvan is de toren in mijn voortuin (figuur 3). Het voert te ver om daar hier verder op in te gaan.
Ik moet nog wel zeggen dat Snelson eind jaren ’60 gelijk had met zijn opmerking. Pas halverwege de jaren ’70 kwamen, met name via de NASA, computerprogramma’s beschikbaar voor het berekenen van dit soort constructies.
Jan W. Marcus
[/read]